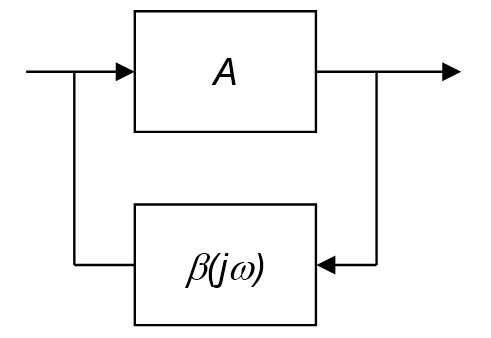
The Barkhausen stability criteria are two conditions used to determine when an electronic circuit will oscillate. They state that if A is the gain of the amplifying element in the circuit and β(jω) is the transfer function of the feedback path, the circuit will sustain steady-state oscillations only at frequencies for which:
The loop gain is equal to unity in absolute magnitude, |βA| = 1
The phase shift around the loop is zero or an integer multiple of 2π, i.e. ∠βA = 2πn for n ∈ 0, 1, 2, 3...
The first criterion will ensure a constant amplitude signal. A number less than 1 will attenuate the signal to zero and a number greater than 1 will amplify the signal to infinity. The second criterion will ensure a stable frequency. For other phase shift values, the sine wave output will be canceled due to the feedback loop.
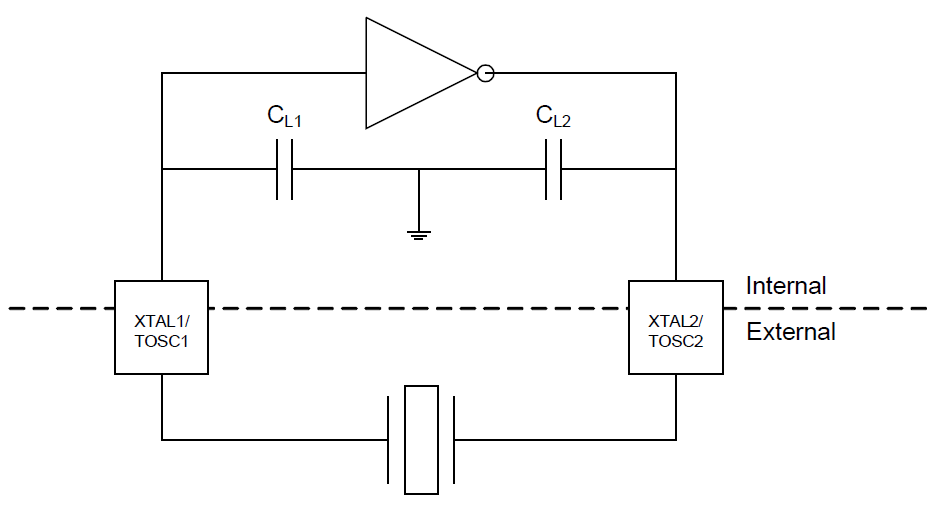
The 32 KHz oscillator in Microchip AVR microcontrollers is shown in Figure 2 and consists of an inverting amplifier (internal) and a crystal (external). Most AVR microcontrollers have an internal capacitive load (CL1 and CL2), so external capacitors are usually not needed. In some cases, however, the external load must be added to meet the crystal specifications. Some AVR microcontrollers can select whether the internal capacitors should be connected or disconnected with the CKOPT fuse. More details can be found in the data sheet of your AVR device.
The inverting amplifier will give a π radian (180 degrees) phase shift, and the remaining π radian phase shift will be provided by the crystal and the capacitive load at 32768 Hz, causing a total phase shift of 2π radian. During start-up, the amplifier output will increase until steady state oscillation is established with a loop gain of 1, causing the Barkhausen criteria to be fulfilled. This is auto-controlled by the AVR microcontroller's oscillator circuitry.